

Últimos Cambios
 Blog personal: El hilo del laberinto
Blog personal: El hilo del laberinto


|

|
Últimos Cambios |
 Blog personal: El hilo del laberinto
Blog personal: El hilo del laberinto
|

|
|
Última Actualización: 8 de enero de 2013
ATENCIÓN: Las medidas de error expuestas en esta página web se corresponden a una latitud de 42 grados norte, la latitud de Vigo (España). Cada latitud tiene su propia figura de error. En general, el error aumenta a medida que aumenta la latitud. Es decir, a medida que nos movemos hacia los polos.
En 2005 publiqué un estudio de la precisión GPS, a partir de medidas realizadas con un receptor GPS (BT77), durante un período continuo de unas 16 horas.
Durante el verano de 2011, utilizando un receptor distinto (chipset MTK), recopilé 500.323 medidas desde el alfeizar de mi ventana en Vigo, tomando una medida cada dos segundos, a lo largo de varias semanas (períodos discontinuos), con intención de publicar un estudio actualizado.
Las diferencias con el estudio anterior son las siguientes:
Por todo ello, los resultados no pueden ni deben compararse directamente con el análisis de 2005. Es conveniente leer y comprender dicho análisis, antes de proceder con este artículo.
El software utilizado para realizar este análisis sale de mi proyecto PyTrek. En concreto, el directorio "precision".
Empecemos por analizar los datos de altura:
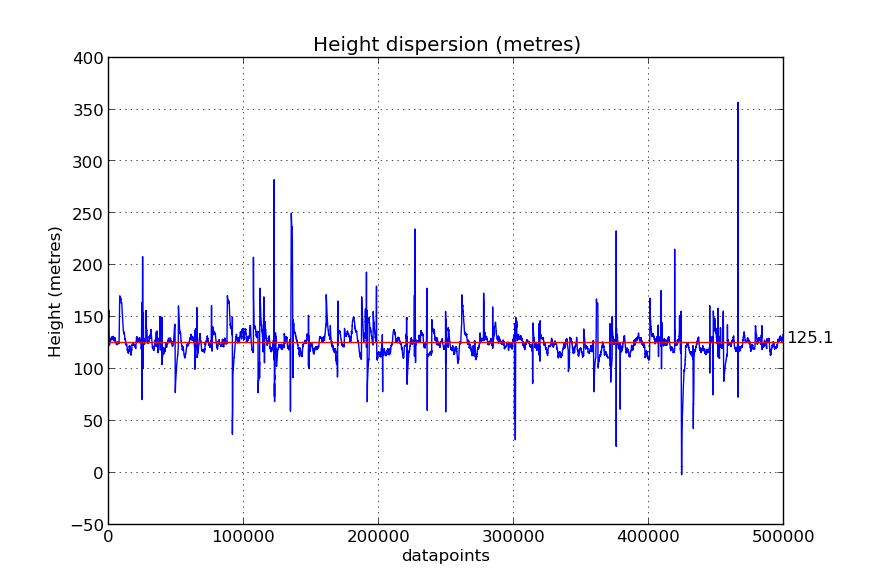
La altura promedio es de 125.1 metros (sin corregir sobre el geoide), pero los errores de altura son muy elevados, y se aprecia claramente la correlación entre muestras. Es decir, es bastante posible que una muestra al azar tenga un error importante, y muestras tomadas en un corto intervalo de tiempo contendrán errores similares.
¿Cuál es el error esperable en una medida al azar?. El gráfico es aproximadamente el siguiente:
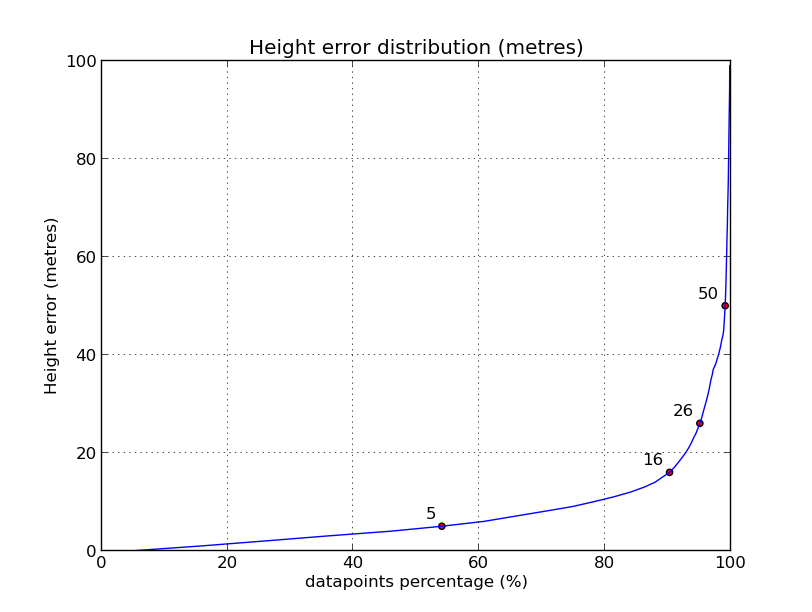
El 54% de las medidas tienen un error de 5 metros o menos. Pero el 90% de las medidas tienen un error de hasta 16 metros, el 95% de las medidas tienen un error de hasta 26 metros, y hay un 1% de medidas con errores superiores a 50 metros.
La gráfica nos da el error estimado en el caso de medidas aisladas. No se puede aplicar en el caso de tomar varias medidas, porque no estamos valorando la correlación que existe entre medidas próximas en el tiempo.
Veamos ahora la precisión horizontal:
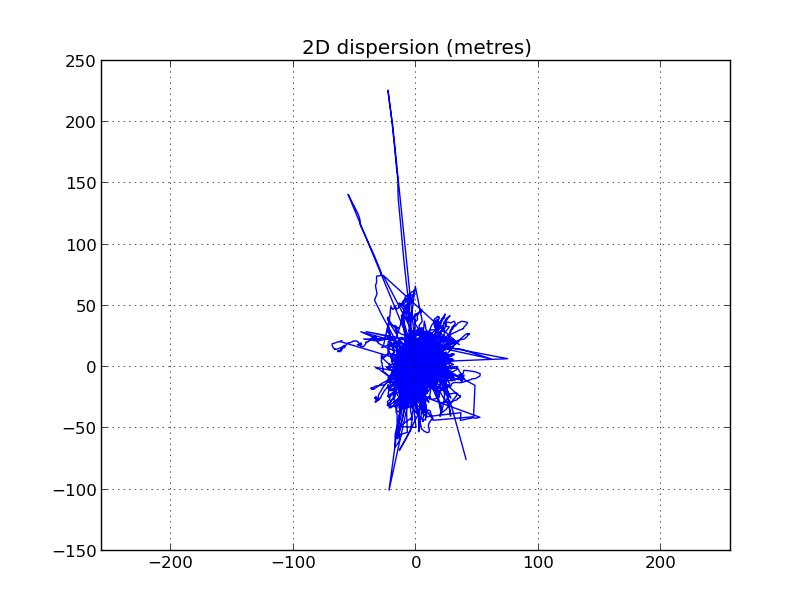
La distribución de error horizontal en tiempo es:
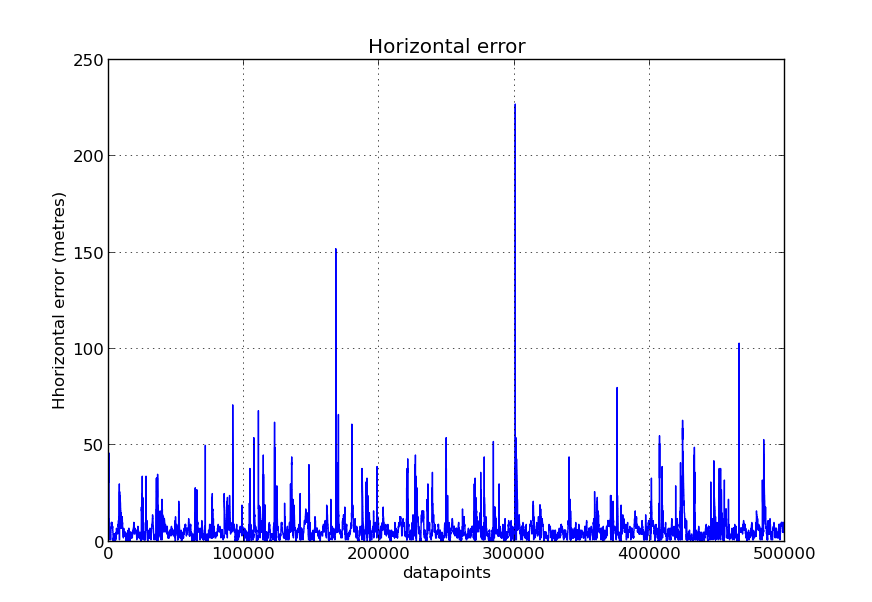
Se ven errores puntuales muy importantes, y una gran correlación temporal.
Calculando el error esperable en una medida al azar, como antes, tenemos:
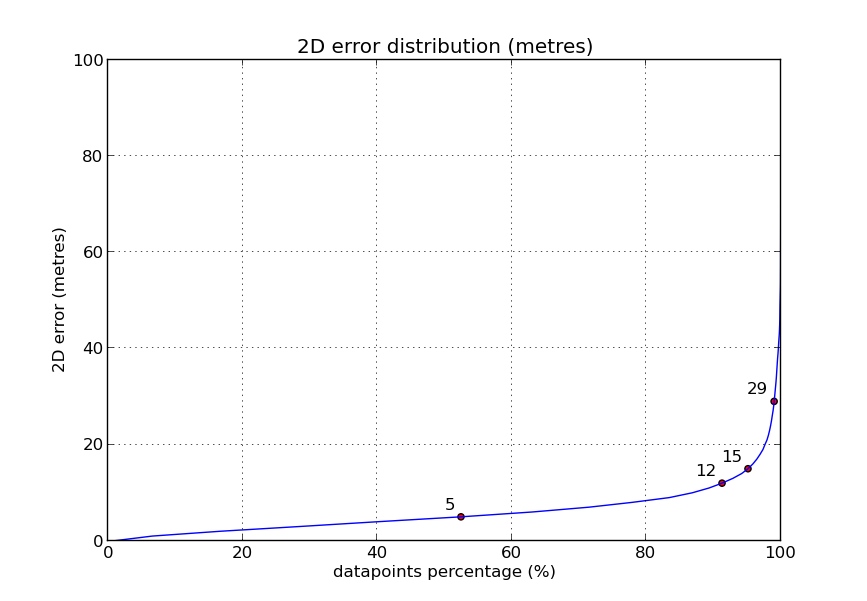
El 52% de las medidas tienen un error de 5 metros o menos. Pero el 90% de las medidas tienen un error de hasta 12 metros, el 95% de las medidas tienen un error de hasta 15 metros, y hay un 1% de medidas con errores superiores a 29 metros.
La gráfica nos da el error estimado en el caso de medidas aisladas. No se puede aplicar en el caso de tomar varias medidas, porque no estamos valorando la correlación que existe entre medidas próximas en el tiempo.
Algunas conclusiones, calcadas a las del informe de 2005:
Como bonus, la distribución de errores, vertical y horizontal:
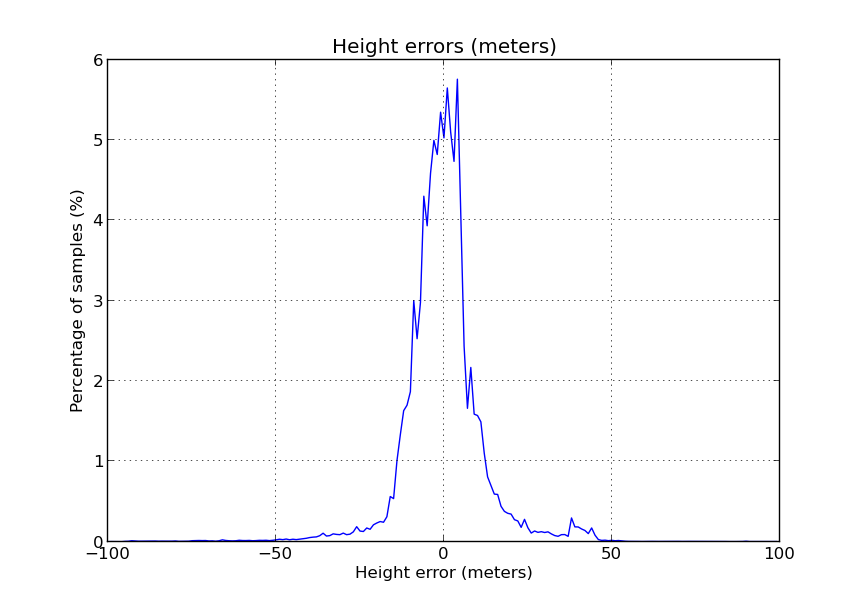
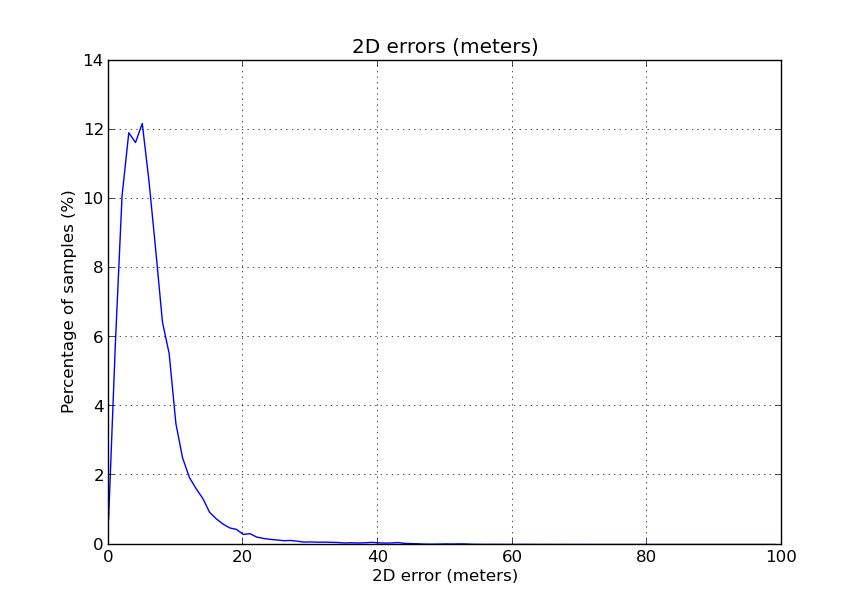
El error vertical parece tener una distribución parecida a la gaussiana, lo que resulta esperable.
En cambio, el error horizontal tiene una moda de 3-5 metros. Es decir, que es más fácil que una medida esté a 3-5 metros de distancia de la posición real, a que esté a una distancia 0-2 metros, por ejemplo. Este resultado es curioso y aparentemente antiintuitivo, pero se corresponde con una distribución de Rayleigh. Las distribuciones de Rayleigh surgen cuando tenemos dos distribuciones gaussianas en dos ejes ortogonales. Es decir, tiene sentido :).
Los errores en sí no son gaussianos, pero es una "aproximación razonable". De hecho, el error de latitud y el de longitud no tienen la misma distribución. Es algo a explorar en un futuro artículo.
Más información sobre los OpenBadges
Donación BitCoin: 19niBN42ac2pqDQFx6GJZxry2JQSFvwAfS
